Quick Sort

Quick sort

1. The best practical choice for sorting
2. Efficient in storage
3. Another Divide-and-conquer based algorithm

• Divide: Partition the array into 2 subarrays around a pivot x. ( […x-1] [x] […x+1] )
• Conquer: Sort the 2 subarrays by recursive calls to quicksort.
• Combine: Trivial (subarrays are already sorted)

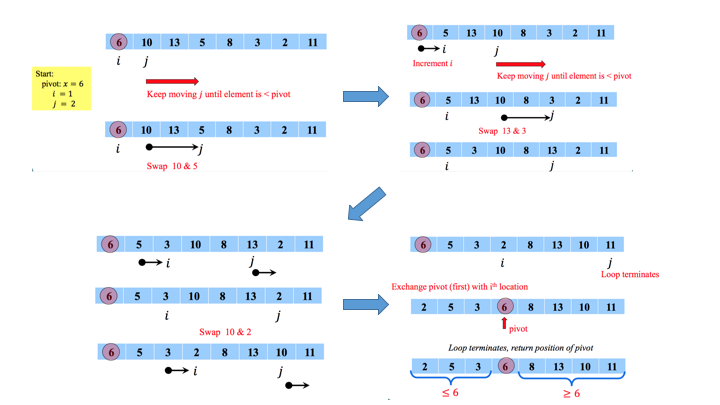
Quick Sort Example

The following shows how quick sort works

Quick Sort Pseudo code

PARTITION(A,p,q)
  x = A[p] // pivot = 1st element of array
  i = p
  for j = p+1 to q
     if A[j] <= x
        i = i+1
        exchange A[i] with A[j]
  exchange A[p] with A[i]                       
  return i //return position of pivot element


QUICKSORT(A,p,r)
  if p<r
     q = PARTITION(A,p,r)
     QUICKSORT(A,p,q-1)
     QUICKSORT(A,q+1,r)

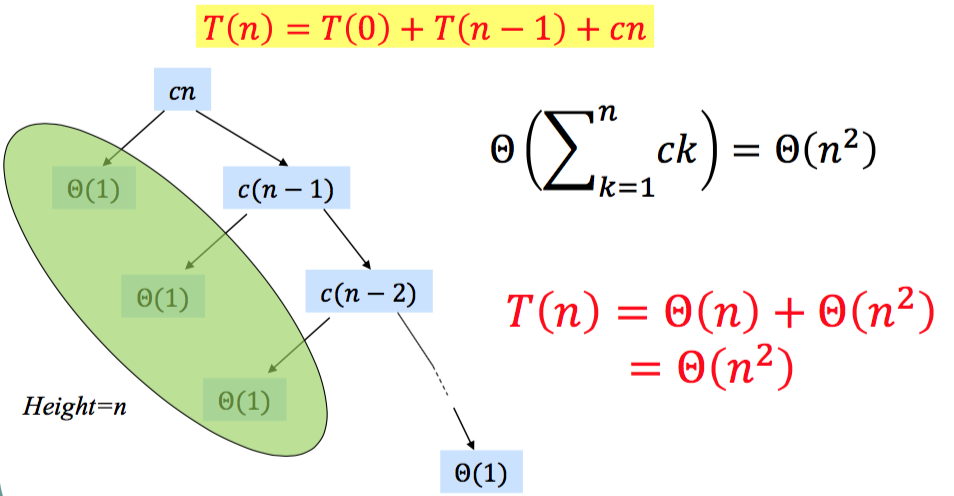
Recurrence equation for Quick Sort (Worst case)

Based on the assumption that each element in the input array is distinct, the location of pivot and the formation of inputs is affecting the performance of quick sort. The worst case input for quick sort is an array sorted in either increasing or decreasing order when the pivot is always the first or the last element. In this case, the pivot happens to be the smallest or biggest element and the pivot becomes the first or the last element splitting the array into zero and the rest.

Solving this recurrence equation with recursion Tree:

Recurrence equation for Quick Sort (Best case)

The best case is when partition splits array evenly.

Average case

The average case input would be any randomly generated arrays and the pivot is at the random position every step.

How to avoid the worst case

• Slow if input is ordered
• Fast otherwise

Answer: Partition around a random pivot element.

Question: Does it always guarantee O(nlgn)? What if the random pivot always happen to be the smallest or biggest?

There is still possibility that randomly picked element is always an extreme.

We can achieve time complexity O(nlgn) even in worst case if we know the median of an unsorted array can be found in linear time.

We can use SELECT algorithm which runs in linear time.

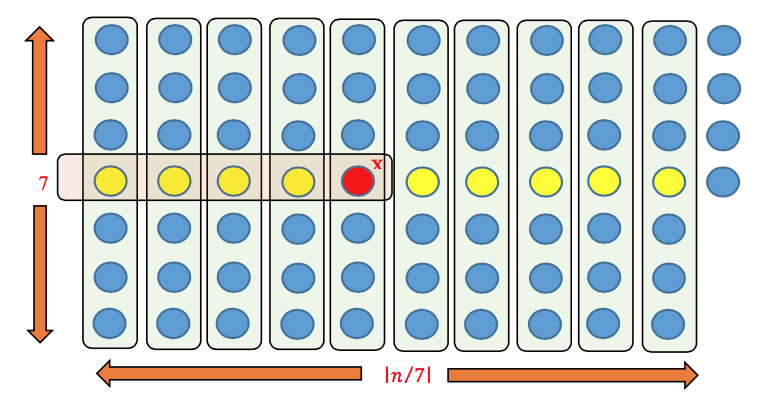
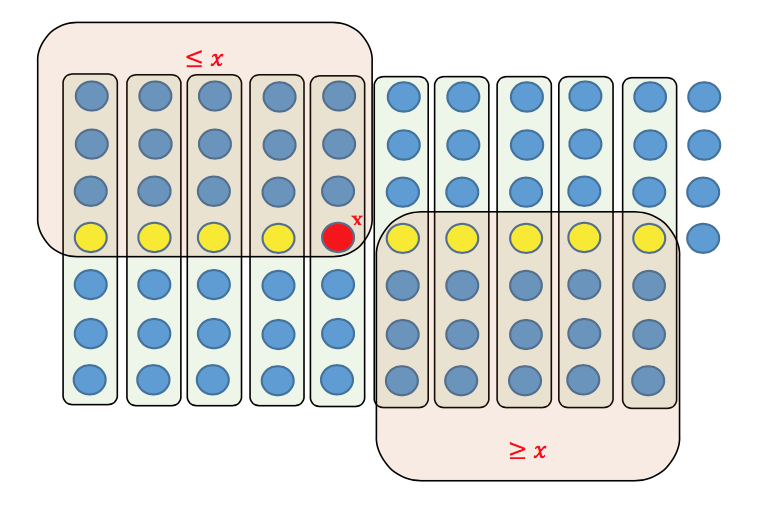
The recurrence equation becomes

T(n) = T(n/2) + T(n/2) + n = 2T(n/2) + n = O(nlgn)