Merge Sort

Divide-and-conquer approach

If there is a problem that cannot be easily solved as it is, we can break the problem into smaller sub-problems if possible (Divide). Then, we solve these sub-problems recursively (Conquer). The solution to the original problem can be created through combining the solutions to the sub-problems (Combine). It is important that how effectively we break the problem into smaller sub-problems. Divide-and-conquer approach is most likely implemented through recursion.

A few examples of the algorithms using Divide-and-conquer approach.

• Quick Sort
• Merge Sort
• Fibonacci sequence
• Exponentiation
• Fast Fourier Transform

Merge sort

Input Array = <5,2,4,7,1,3,2,6>

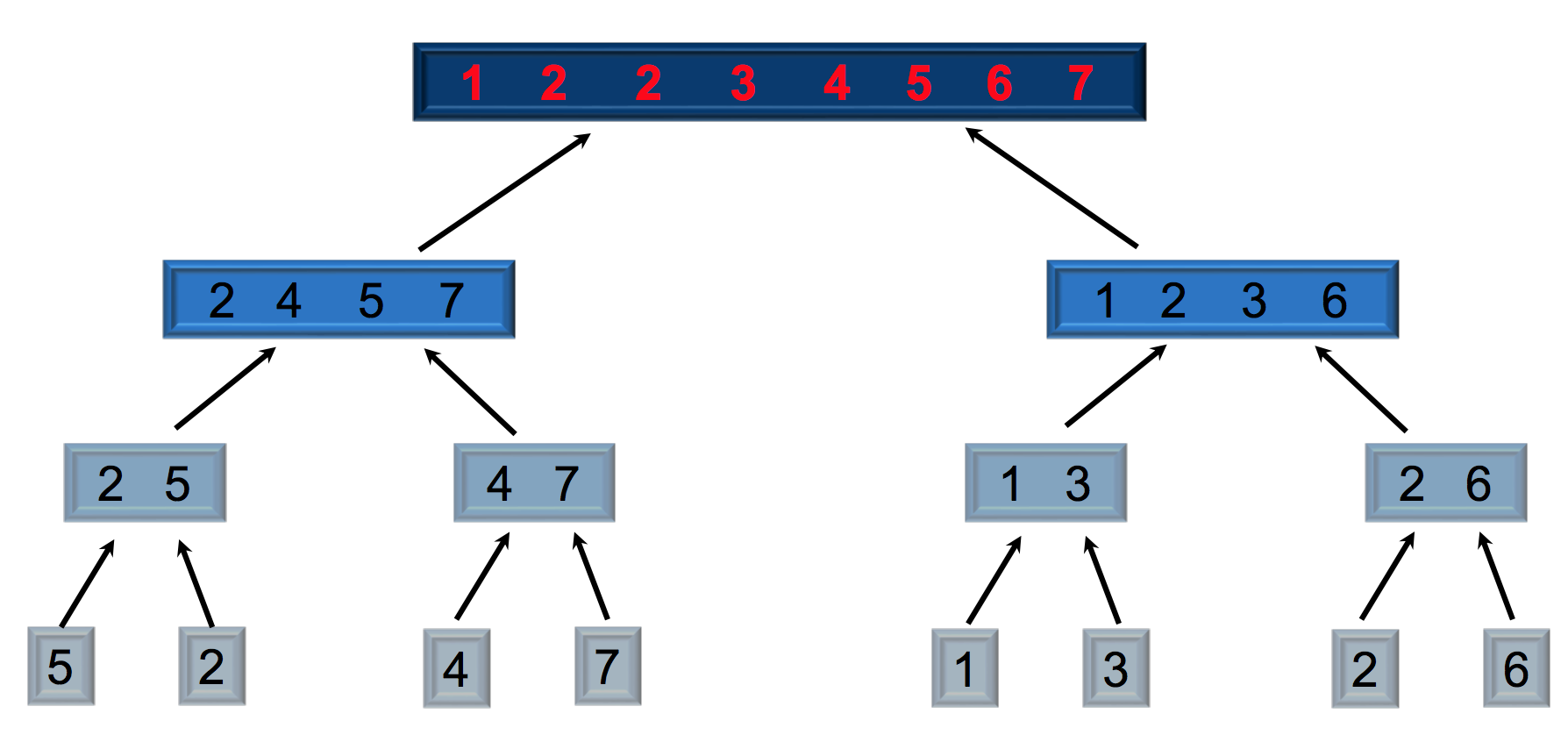
Merge Sort Pseudo code

T(n)           MERGE-SORT A[1 ... n]
O(1)             If n=1, done                        
T(n/2)+T(n/2)    recursively sort A[1 ... n/2] and A[n/2+1 ... n]
O(n)             MERGE the 2 sorted lists

Recurrence equation for Merge Sort

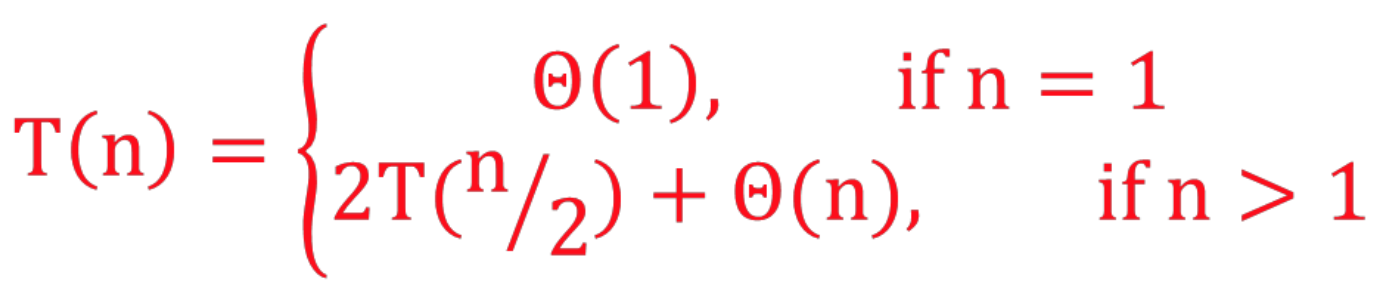
T(n) = 2T(n/2) + O(n)

How to solve recurrences?

3 methods for solving recurrences (Obtaining O-notation)

• Substitution method
• Recursion-tree method
• Master method

Substitution method (a.k.a making a good guess method)

1. Guess the form of the solutions
2. Verify if recurrence is satisfied
3. Solve for constants

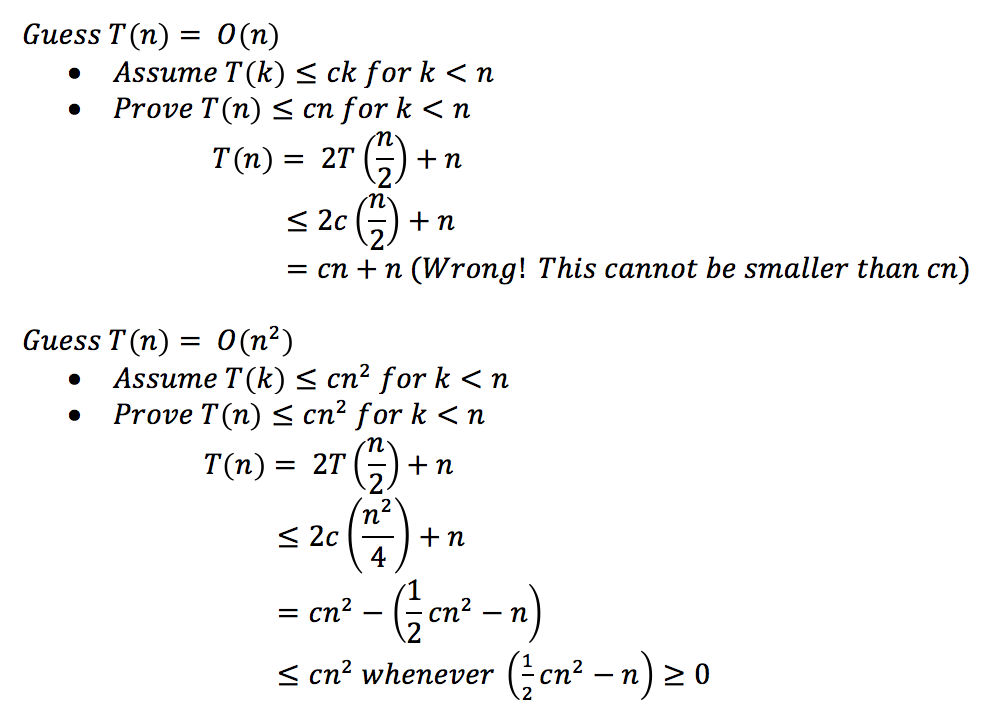
Can we have a tighter bound?

Recursion-tree method

Models the costs of a recursion execution of an algorithm

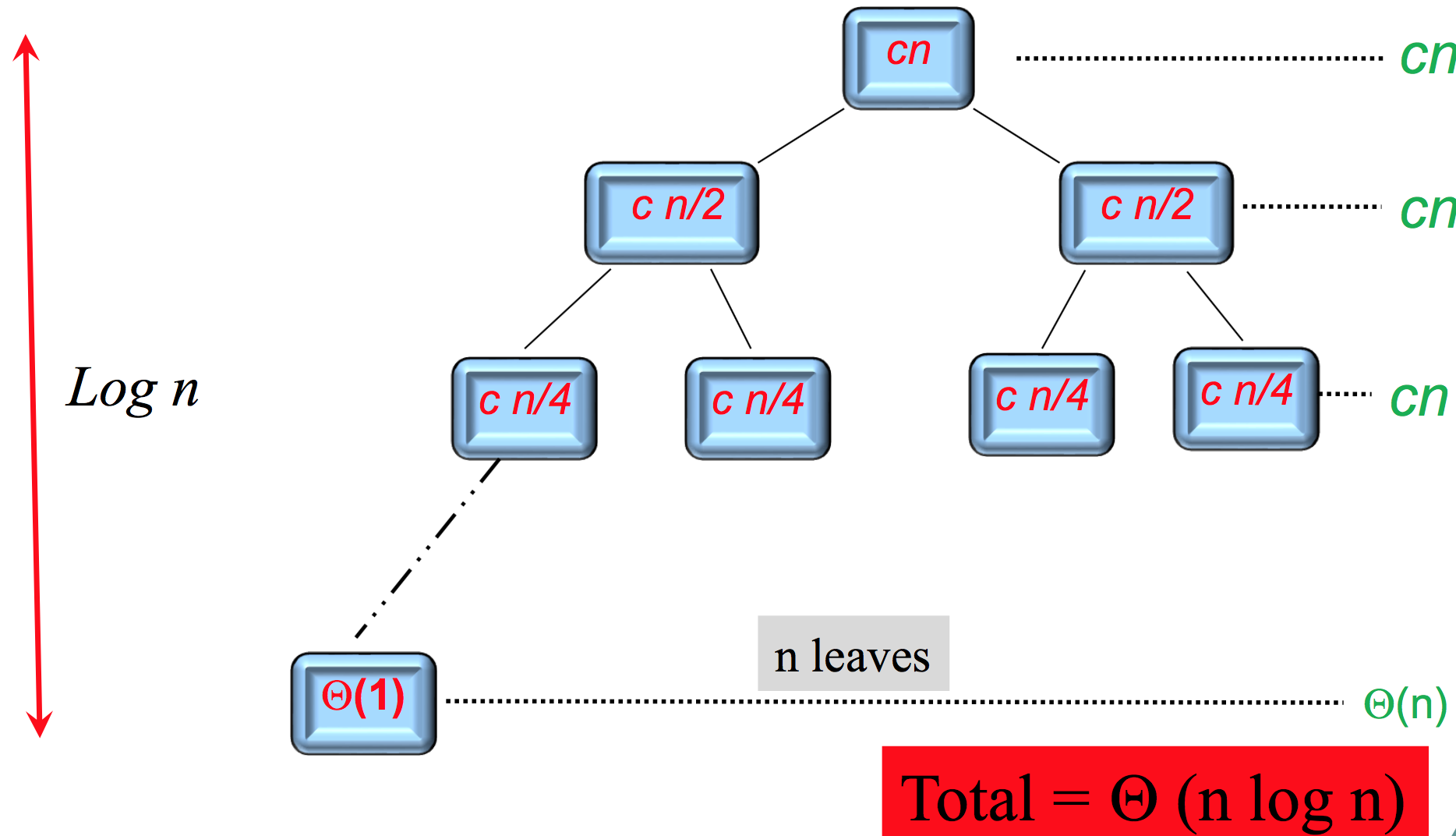
Master method

Master method only applies to a particular family of recurrences of the form.

How to solve with master method (pre-defined 3 cases)

Solve MergeSort using Master method

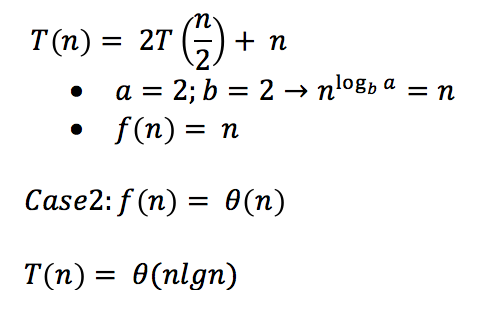
The merge sort implementation in Lua.

local mergeSort = {}

function mergeSort.merge(array, p, q, r)
  local n1 = q-p+1
  local n2 = r-q
  local left = {}
  local right = {}

  for i=1, n1 do
    left[i] = array[p+i-1]
  end
  for i=1, n2 do
    right[i] = array[q+i]
  end

  left[n1+1] = math.huge
  right[n2+1] = math.huge

  local i=1
  local j=1

  for k=p, r do
    if left[i]<=right[j] then
      array[k] = left[i]
      i=i+1
    else
      array[k] = right[j]
      j=j+1
    end
  end
  return array
end

function mergeSort.sort(array, p, r)
  if p < r then
    local q = math.floor((p + r)/2)
    mergeSort.sort(array, p, q)
    mergeSort.sort(array, q+1, r)
    mergeSort.merge(array, p, q, r)
  end
  return array
end

return mergeSort

The unit test of insertion sort with Lua Busted

local mergeSort = require('mergeSort')

describe('mergeSort', function()
  describe('merge', function()
    it('should merge empty arrays', function()
      assert.are.same({1, 2, 3, 4}, mergeSort.merge({1, 2, 3, 4}, 1, 2, 4))
    end)
  end)

  describe('sort', function()
    it('should sort over an empty array', function()
      assert.are.same({ }, mergeSort.sort({ }, 0, 0))
    end)

    it('should sort over an array with a single element', function()
      assert.are.same({1}, mergeSort.sort({1}, 1, 1))
    end)

    it('should sort over an array with several elements', function()
      assert.are.same({ 1, 2, 3 }, mergeSort.sort({ 3, 2, 1 }, 1, 3))
    end)

    it('should sort over an array with same elements', function()
      assert.are.same({ 2, 2, 3, 3, 4 }, mergeSort.sort({ 3, 2, 4, 2, 3 }, 1, 5))
    end)

    it('should not modify the input array', function()
      local input = { 1, 2, 3 }
      mergeSort.sort(input, 1, 3)
      assert.are.same({ 1, 2, 3 }, input)
    end)
  end)
end)

Merge Sort time analysis

For merge sort, any inputs with the size n regardless of input pre-sorted or not would perform the same asymptotically because this algorithm is based on divide-and-conquer. No matter what inputs are, it will still make the same recursive calls to divide array into two halves and take the linear time to merge the values. The time complexity for all cases would be O(nlgn) for any inputs; thus, the processing time for this case will grow as the rate of as n increase.