Insertion Sort

Loop Invariants

In computer science, a loop invariant is a property of a program loop that is true before (and after) each iteration. It is a logical assertion, sometimes checked within the code by an assertion call. Knowing its invariant(s) is essential in understanding the effect of a loop [^1].

Basically, loop invariants is used to prove the correctness of loop algorithms. In a loop, the state always changes, but a loop invariant is true for each iteration.

Three categories to satisfy to prove loop invariants:

1) Initialization: Check if it is true prior to the initial iteration.

2) Maintenance: Check if it is true before an iteration of the loop, it remains true before the next iteration.

3) Termination: When the loop ends, we should get a meaningful and useful result which will help to show the correctness of the algorithm.

Insertion sort

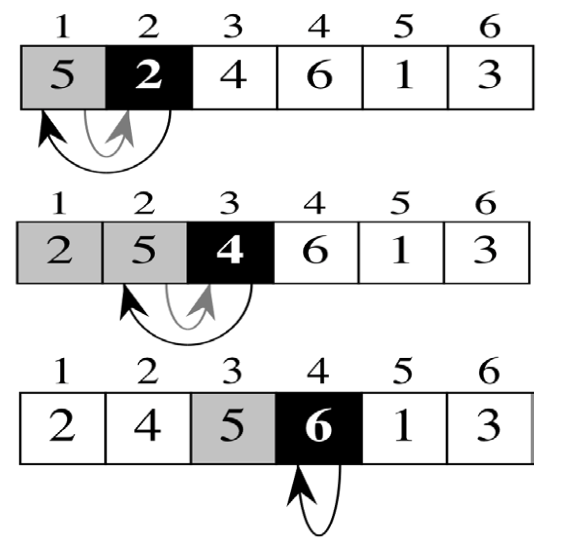
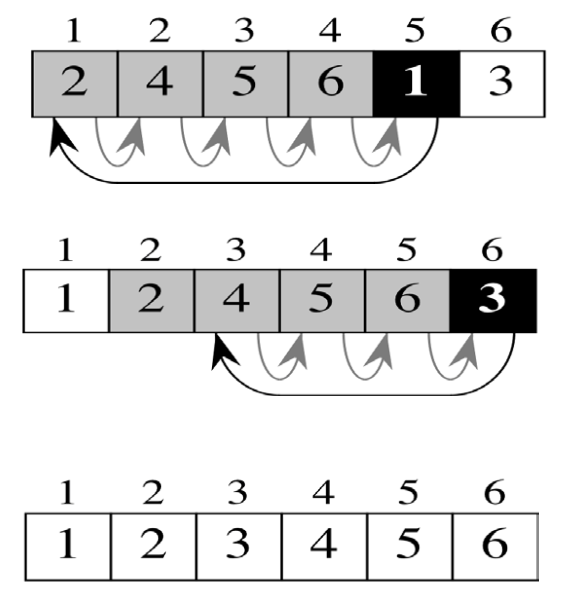
The insertion sort implementation in Lua.

function insertionSort(array)
  for j = 2, #array do
    local key = array[j]
    local i = j - 1
    while i > 0 and array[i] > key do
      array[i + 1] = array[i]
      i = i - 1
    end
    array[i + 1] = key
  end
  return array
end

return insertionSort

Loop Invariant in Insertion sort

function insertionSort(array)   
-- Initialization: before the initial interval, j = 2. array[1] should be sorted, and it surely is.      
  for j = 2, #array do            
    local key = array[j]
    local i = j - 1

    -- Maintenance: As loop goes, j will be incremented and array[1...j-1] is sorted.
    while i > 0 and array[i] > key do
      array[i + 1] = array[i]
      i = i - 1
    end
    array[i + 1] = key
  end

  -- Termination: the loop ends when j = length(array) + 1, and array[1...j] is sorted.
  return array
end

return insertionSort

The unit test of insertion sort with Lua Busted

local insertionSort = require('insertionSort')

describe('insertionSort', function()
  it('should sort over an empty array', function()
    assert.are.same({}, insertionSort({}))
  end)

  it('should sort over an array with a single element', function()
    assert.are.same({ 3 }, insertionSort({ 3 }))
  end)

  it('should sort over an array with several elements', function()
    assert.are.same({ 1, 2, 3 }, insertionSort({ 3, 2, 1 }))
  end)

  it('should sort over an array with same elements', function()
    assert.are.same({ 2, 2, 3, 3, 4 }, insertionSort({ 3, 2, 4, 2, 3 }))
  end)

  it('should not modify the input array', function()
    local input = { 1, 2, 3 }
    insertionSort(input)
    assert.are.same({ 1, 2, 3 }, input)
  end)
end)

Insertion Sort time analysis

The best case :

The best case input is an array sorted in increasing order. No elements in the left of a key is smaller if the array is pre-sorted in increasing order; therefore, no elements would be shifted while iterating through the array. In this case, the time complexity would be O(n); thus, the processing time of the best case should grow linearly as n increase.

The worst case :

The worst case input is an array sorted in decreasing order. A key element is always smaller than the one that is in its left causing the one-position shift of elements for every loop iterating though the array; thus, the time complexity in this case would be O(n^2). The processing time for this case will grow exponentially as the rate of as n increase.

The average case :

The average case input would be any randomly generated arrays except for the ones that happens to be generated as the pre-sorted array. The performance would be dependent on the degree of how close to the input array being sorted. For instance, the almost sorted input in increasing order would perform as close to the best case. Except for this case, assuming the half of the input array is sorted, the time complexity would be still O(n^2) due to the shift and loop iteration; thus, the processing time for this case will still grow exponentially as the rate of as n increase.

Reference

[^1] https://en.wikipedia.org/wiki/Loop_invariant