BFS and DFS
BFS and DFS for solving TSP
The following figure is the graphic representation of how BFS works. It navigates each city in the first depth starting from the start city. Then, it continues searching the second and third depth until every city has been scanned.

The below figure shows how DFS operates. The searching process is done by following through each branch of the search tree until the leaf of this tree has been reached. If the search pointer reaches the leaf of the branch, it moves to the nearest parent and continues to search from there.

The performance of both algorithms to find the shortest path is heavily dependent on the depth of the goal city in a search tree and a branching factor, considering the time complexity of O(b^d) where b is a branching factor and d is the depth. BFS is expected to perform better than DFS in case the target is close to the start city. On the other hand, DFS might possibly perform better if the target is somewhere deep in a search tree.
Definition Lists
- BFS
- Breadth First Search
- DFS
- Depth First Search
BFS and DFS to solve TSP in Matlab
The input example for 11 cities
The coordinates of 11 cities used in the example.
| Cities | X coordinate | Y coordinate |
|---|---|---|
| City 1 | 5.6818 | 63.8604 |
| City 2 | 11.8506 | 83.9836 |
| City 3 | 13.7987 | 65.0924 |
| City 4 | 16.8831 | 40.4517 |
| City 5 | 23.7825 | 56.2628 |
| City 6 | 25.0000 | 31.2115 |
| City 7 | 29.9513 | 41.6838 |
| City 8 | 31.3312 | 25.2567 |
| City 9 | 37.1753 | 37.5770 |
| City 10 | 39.9351 | 19.0965 |
| City 11 | 46.8344 | 29.9795 |
The following table represents the one-way path connection of cities (left = from and top = to). For instance, the first row represents that the transition is allowed from city 1 to one of city 2, 3 and 4. From the given table, branching factor of the search tree is 3.
| Cities | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | X | X | X | ||||||||
| 2 | X | ||||||||||
| 3 | X | X | |||||||||
| 4 | X | X | X | ||||||||
| 5 | X | X | |||||||||
| 6 | X | ||||||||||
| 7 | X | X | |||||||||
| 8 | X | X | X | ||||||||
| 9 | X | ||||||||||
| 10 | X |
I hard-coded the both above tables as below for the demonstration purpose.
The following code block is the implementation of BFS to solve TSP in Matlab.
The following code block is the implementation of DFS to solve TSP in Matlab.
The implementation of DFS can be done by calling a function recursively until every path to the target city has been found.
The distance between two cities are calculated as below.
The figure below shows the shortest path and its length from the 11 city dataset input.
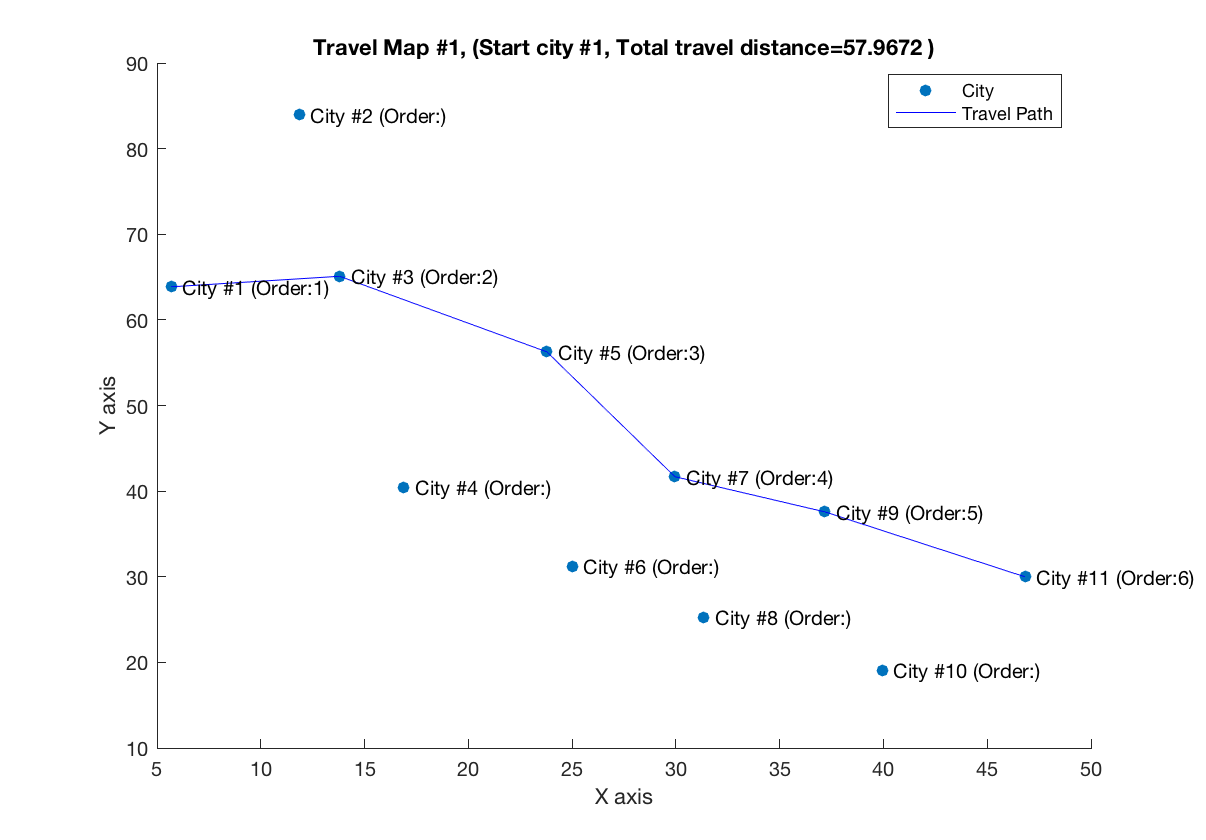
Both BFS and DFS shows the identical results, but the searching transition history is different as below;
| DFS | BFS |
|---|---|
| Transit from 1 to 2 : count = 1 | Transit from 1 to 2 : count = 1 |
| Transit from 2 to 3 : count = 2 | Transit from 1 to 3 : count = 2 |
| Transit from 3 to 4 : count = 3 | Transit from 1 to 4 : count = 3 |
| Transit from 4 to 5 : count = 4 | Transit from 2 to 3 : count = 4 |
| Transit from 5 to 7 : count = 5 | Transit from 3 to 4 : count = 5 |
| Transit from 7 to 9 : count = 6 | Transit from 3 to 5 : count = 6 |
| Transit from 9 to 11 : count = 7 | Transit from 4 to 5 : count = 7 |
| Transit from 7 to 10 : count = 8 | Transit from 4 to 6 : count = 8 |
| Transit from 10 to 11 : count = 9 | Transit from 4 to 7 : count = 9 |
| Transit from 5 to 8 : count = 10 | Transit from 5 to 7 : count = 10 |
| Transit from 8 to 9 : count = 11 | Transit from 5 to 8 : count = 11 |
| Transit from 9 to 11 : count = 12 | Transit from 6 to 8 : count = 12 |
| Transit from 8 to 10 : count = 13 | Transit from 7 to 9 : count = 13 |
| Transit from 10 to 11 : count = 14 | Transit from 7 to 10 : count = 14 |
| Transit from 8 to 11 : count = 15 | Transit from 7 to 9 : count = 15 |
| Transit from 4 to 6 : count = 16 | Transit from 7 to 10 : count = 16 |
| Transit from 6 to 8 : count = 17 | Transit from 8 to 9 : count = 17 |
| Transit from 8 to 9 : count = 18 | Transit from 8 to 10 : count = 18 |
| Transit from 9 to 11 : count = 19 | Transit from 8 to 11 : count = 19 |
| Transit from 8 to 10 : count = 20 | Transit from 8 to 9 : count = 20 |
| Transit from 10 to 11 : count = 21 | Transit from 8 to 10 : count = 21 |
| Transit from 8 to 11 : count = 22 | Transit from 8 to 11 : count = 22 |
| Transit from 4 to 7 : count = 23 | Transit from 9 to 11 : count = 23 |
| Transit from 7 to 9 : count = 24 | Transit from 10 to 11 : count = 24 |
| Transit from 9 to 11 : count = 25 | Transit from 10 to 11 : count = 25 |
| Transit from 7 to 10 : count = 26 | |
| Transit from 10 to 11 : count = 27 | |
| Transit from 3 to 5 : count = 28 | |
| Transit from 5 to 7 : count = 29 | |
| Transit from 7 to 9 : count = 30 | |
| Transit from 9 to 11 : count = 31 | |
| Transit from 7 to 10 : count = 32 | |
| Transit from 10 to 11 : count = 33 | |
| Transit from 5 to 8 : count = 34 | |
| Transit from 8 to 9 : count = 35 | |
| Transit from 9 to 11 : count = 36 | |
| Transit from 8 to 10 : count = 37 | |
| Transit from 10 to 11 : count = 38 | |
| Transit from 8 to 11 : count = 39 | |
| Transit from 1 to 3 : count = 40 | |
| Transit from 3 to 4 : count = 41 | |
| Transit from 4 to 5 : count = 42 | |
| Transit from 5 to 7 : count = 43 | |
| Transit from 7 to 9 : count = 44 | |
| Transit from 9 to 11 : count = 45 | |
| Transit from 7 to 10 : count = 46 | |
| Transit from 10 to 11 : count = 47 | |
| Transit from 5 to 8 : count = 48 | |
| Transit from 8 to 9 : count = 49 | |
| Transit from 9 to 11 : count = 50 | |
| Transit from 8 to 10 : count = 51 | |
| Transit from 10 to 11 : count = 52 | |
| Transit from 8 to 11 : count = 53 | |
| Transit from 4 to 6 : count = 54 | |
| Transit from 6 to 8 : count = 55 | |
| Transit from 8 to 9 : count = 56 | |
| Transit from 9 to 11 : count = 57 | |
| Transit from 8 to 10 : count = 58 | |
| Transit from 10 to 11 : count = 59 | |
| Transit from 8 to 11 : count = 60 | |
| Transit from 4 to 7 : count = 61 | |
| Transit from 7 to 9 : count = 62 | |
| Transit from 9 to 11 : count = 63 | |
| Transit from 7 to 10 : count = 64 | |
| Transit from 10 to 11 : count = 65 | |
| Transit from 3 to 5 : count = 66 | |
| Transit from 5 to 7 : count = 67 | |
| Transit from 7 to 9 : count = 68 | |
| Transit from 9 to 11 : count = 69 | |
| Transit from 7 to 10 : count = 70 | |
| Transit from 10 to 11 : count = 71 | |
| Transit from 5 to 8 : count = 72 | |
| Transit from 8 to 9 : count = 73 | |
| Transit from 9 to 11 : count = 74 | |
| Transit from 8 to 10 : count = 75 | |
| Transit from 10 to 11 : count = 76 | |
| Transit from 8 to 11 : count = 77 | |
| Transit from 1 to 4 : count = 78 | |
| Transit from 4 to 5 : count = 79 | |
| Transit from 5 to 7 : count = 80 | |
| Transit from 7 to 9 : count = 81 | |
| Transit from 9 to 11 : count = 82 | |
| Transit from 7 to 10 : count = 83 | |
| Transit from 10 to 11 : count = 84 | |
| Transit from 5 to 8 : count = 85 | |
| Transit from 8 to 9 : count = 86 | |
| Transit from 9 to 11 : count = 87 | |
| Transit from 8 to 10 : count = 88 | |
| Transit from 10 to 11 : count = 89 | |
| Transit from 8 to 11 : count = 90 | |
| Transit from 4 to 6 : count = 91 | |
| Transit from 6 to 8 : count = 92 | |
| Transit from 8 to 9 : count = 93 | |
| Transit from 9 to 11 : count = 94 | |
| Transit from 8 to 10 : count = 95 | |
| Transit from 10 to 11 : count = 96 | |
| Transit from 8 to 11 : count = 97 | |
| Transit from 4 to 7 : count = 98 | |
| Transit from 7 to 9 : count = 99 | |
| Transit from 9 to 11 : count = 100 | |
| Transit from 7 to 10 : count = 101 | |
| Transit from 10 to 11 : count = 102 |