Brute Force Search
Brute Force Search for solving TSP
To find the minimum cost solution to a Travelling Salesperson Problem, brute force search could be the most simple approach. This approach calculates the distance of each permutation path set, in other words, it simply checks every single path. It does always find the shortest path, but the dramatic increases in the time cost is unavoidable as the input size grows. Consider the input with 10 cities. the total number of possible complete path is as large as 3628800. This number can go up to 39916800 by adding just one more city.
Definition Lists
TSP : Travelling Salesperson Problem
Brute Force to solve TSP in Matlab
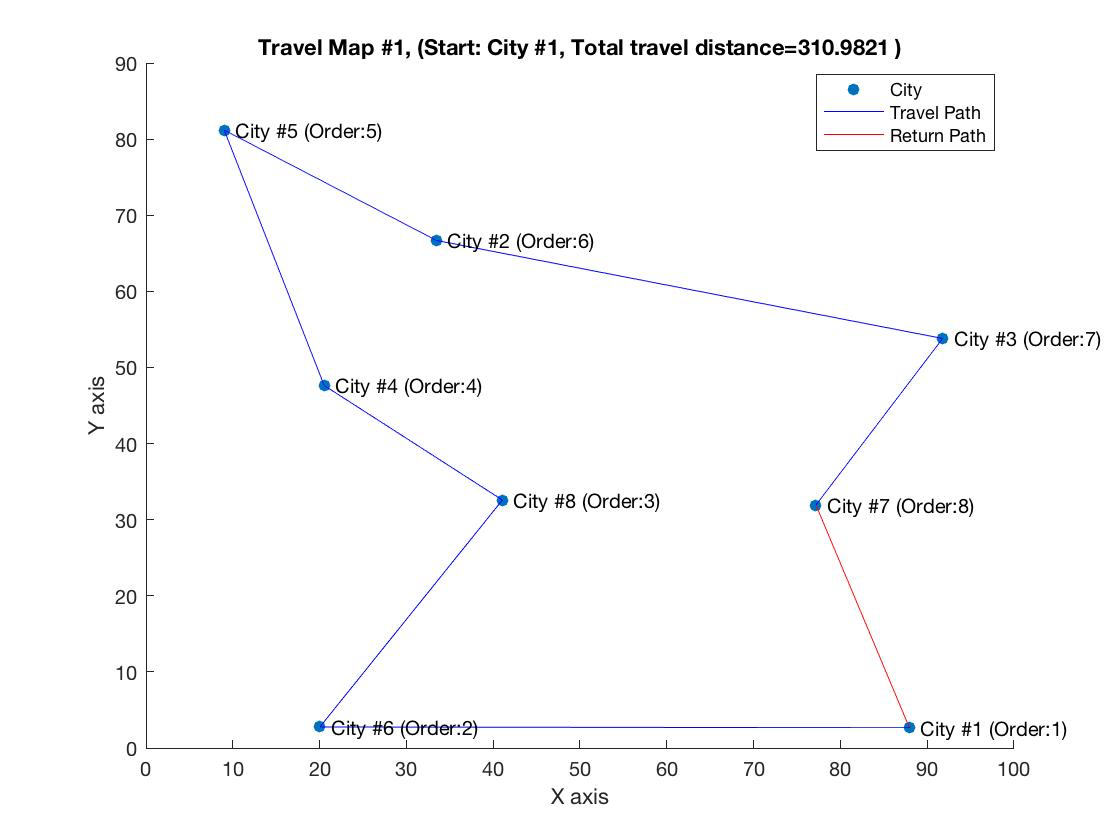
The input example for 8 cities
| Cities | X coordinate | Y coordinate |
|---|---|---|
| City 1 | 87.9512 | 2.6581 |
| City 2 | 33.4665 | 66.6829 |
| City 3 | 91.7783 | 53.8071 |
| City 4 | 20.5267 | 47.6332 |
| City 5 | 9.0060 | 81.1853 |
| City 6 | 20.0323 | 2.7619 |
| City 7 | 77.1813 | 31.9223 |
| City 8 | 41.0596 | 32.5785 |
With the coordinate date of each city, the first possible path is generated from the user-selected starting city in ascending order (e.g., [4 1 2 3 5 6] where the starting city is 4). This sorting is needed to find all the possible paths from the starting city by getting the next permutation set in lexicographic order. Once the distance evaluation of each path is completed, the shortest path and its distance is identified.
The following code block is the implementation of Brute Force to solve TSP in Matlab.
The implementation of a permutation is done with the lexicographic order algorithm generating the next permutation set of an input array.
The figure below shows the shortest path and its length from randomly generated 8 city dataset.